벡터들의 덧샘 연산과 선형 결합이 기하학적으로 어떻게 표현될 수 있는지 알아볼 수 있는 문제를 풀어보겠습니다. 문제들은 Gilbert Strang의 교과서의 것입니다.
1. 다음 벡터들의 모든 선형 결합을 선, 평면, $R^{3}$ 등으로 표현하라:
(a) $\begin{bmatrix} \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \end{bmatrix}$와 $\begin{bmatrix} \begin{array}{r} 3 \\ 6 \\ 9 \end{array} \end{bmatrix}$
답) 벡터가 두 개이지만, 두번째 벡터($y$)는 첫번째 벡터($x$)와 방향이 같습니다.
즉, $y$ = $3x$.
따라서 두 벡터의 모든 선형 결합은 $cx$이 됩니다. 이는 $R^{3}$에서 원점을 지나는 선으로 표현됩니다.
(b) $\begin{bmatrix} \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \end{bmatrix}$와 $\begin{bmatrix} \begin{array}{r} 0 \\ 2 \\ 3 \end{array} \end{bmatrix}$
답) (a)의 경우와는 다르게 두 벡터는 방향이 다릅니다.
다시 말하면, 한 벡터는 다른 벡터의 선형 결합이 될 수 없습니다.
따라서 두 벡터의 모든 선형 결합은 $R^{3}$에서 원점을 평면으로 표현됩니다.
(c) $\begin{bmatrix} \begin{array}{r} 2 \\ 0 \\ 0 \end{array} \end{bmatrix}$와 $\begin{bmatrix} \begin{array}{r} 0 \\ 2 \\ 2 \end{array} \end{bmatrix}$와 $\begin{bmatrix} \begin{array}{r} 2 \\ 2 \\ 3 \end{array} \end{bmatrix}$
답) 이 경우 역시 한 벡터를 다른 두 벡터의 선형 결합으로 쓸 수 없습니다.
즉, 세 벡터는 모두 방향이 다릅니다.
따라서 위 벡터들의 모든 선형 결합은 $R^{3}$가 됩니다.
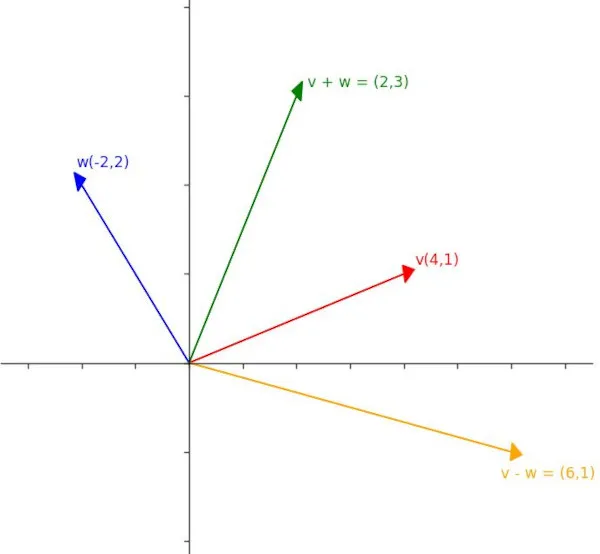
2. 다음 벡터 $v$, $w$, $v$ + $w$, $v$ – $w$ 를 $xy$평면 상에 그려라.
$v$ = $\begin{bmatrix} \begin{array}{r} 4 \\ 1 \end{array} \end{bmatrix}$ $w$ = $\begin{bmatrix} \begin{array}{r} -2 \\ 2 \end{array} \end{bmatrix}$.
답) $v$ + $w$ = $\begin{bmatrix} \begin{array}{r} 4 - 2 \\ 1 + 2 \end{array} \end{bmatrix}$ = $\begin{bmatrix} \begin{array}{r} 2 \\ 3 \end{array} \end{bmatrix}$
$v$ – $w$ = $\begin{bmatrix} \begin{array}{r} 4 + 2 \\ 1 - 2 \end{array} \end{bmatrix}$ = $\begin{bmatrix} \begin{array}{r} 6 \\ -1 \end{array} \end{bmatrix}$
$v$, $w$, $v$ + $w$, $v$ – $w$ 를 $xy$평면 상에 그리면 아래와 같습니다.
'선형대수 > 문제풀이' 카테고리의 다른 글
| 1.1e 벡터의 연산, 시계 문제 (0) | 2022.09.03 |
|---|---|
| 1.1d 단위 벡터, 정육면체, xyz 공간 문제 (0) | 2022.09.02 |
| 1.1c 벡터의 성분, 선형 결합(문제6~9) (0) | 2022.09.01 |
| 1.1b 벡터의 덧셈, 뺄셈(문제3~5) (1) | 2022.09.01 |
| 1장 벡터 행렬 문제 풀이 (0) | 2022.01.11 |



댓글