벡터는 선형 대수학에서 매우 중요한 개념입니다. 벡터는 크기와 방향을 갖는 개체이며, 좌표계에서 화살표 등으로 시각화되기도 합니다. 벡터들의 선형 결합은 선형 대수학의 중요한 시작점이 됩니다. 이 포스팅에서는 벡터 덧셈, 스칼라 곱셈, 그리고 선형 결합의 의미 등을 알아보겠습니다.
벡터(vector)
벡터는 크기와 방향을 갖는 개체입니다.
보통 좌표계에서 화살표로 표현됩니다.
선형 대수학에는 벡터에 대한 두 가지 중요한 연산이 있습니다.
먼저, 두 벡터 $v$와 $w$ 가 있다고 가정합시다.
그러면, 첫째 연산은 벡터 덧셈 (vector addition)입니다.
이 연산은 벡터들을 더하여 $v$ + $w$를 얻습니다.
두 번째 연산은 스칼라 곱셈 (scalar multiplication)입니다.
이 연산은 벡터에 스칼라라고 불리는 숫자 $c$를 벡터 $v$에 곱하여 $cv$를 얻는 것입니다.
여기서 스칼라는 크기만 갖는 숫자로 크기와 방향을 갖는 벡터와 대비됩니다.
벡터 $v$와 $w$에 각각 스칼라 $c$와 $d$를 곱하고, 이들을 더하면 $cv$ + $dw$를 얻습니다. 이 $cv$ + $dw$는 새로운 벡터이며, $v$와 $w$의 선형 결합이라고 합니다.
예를 들어, 두 벡터 $v$ = $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 와 $w$ = $\begin{bmatrix} 2 \\ 3 \end{bmatrix}$ 있다고 가정하면,
두 벡터의 합은 $v$ + $w$ = $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ + $\begin{bmatrix} 2 \\ 3 \end{bmatrix}$ = $\begin{bmatrix} 3 \\ 4 \end{bmatrix}$.
이 합은 $c$ = $d$ = 1인 두 벡터의 선형 결합입니다.
만약, $c$ = 2, $d$ = 1 이라면, 이에 대응하는 선형 결합은 2$v$ + $w$ = $\begin{bmatrix} 4 \\ 5 \end{bmatrix}$ 입니다.
벡터는 아래 그림과 같이 좌표계에 그릴 수 있습니다.
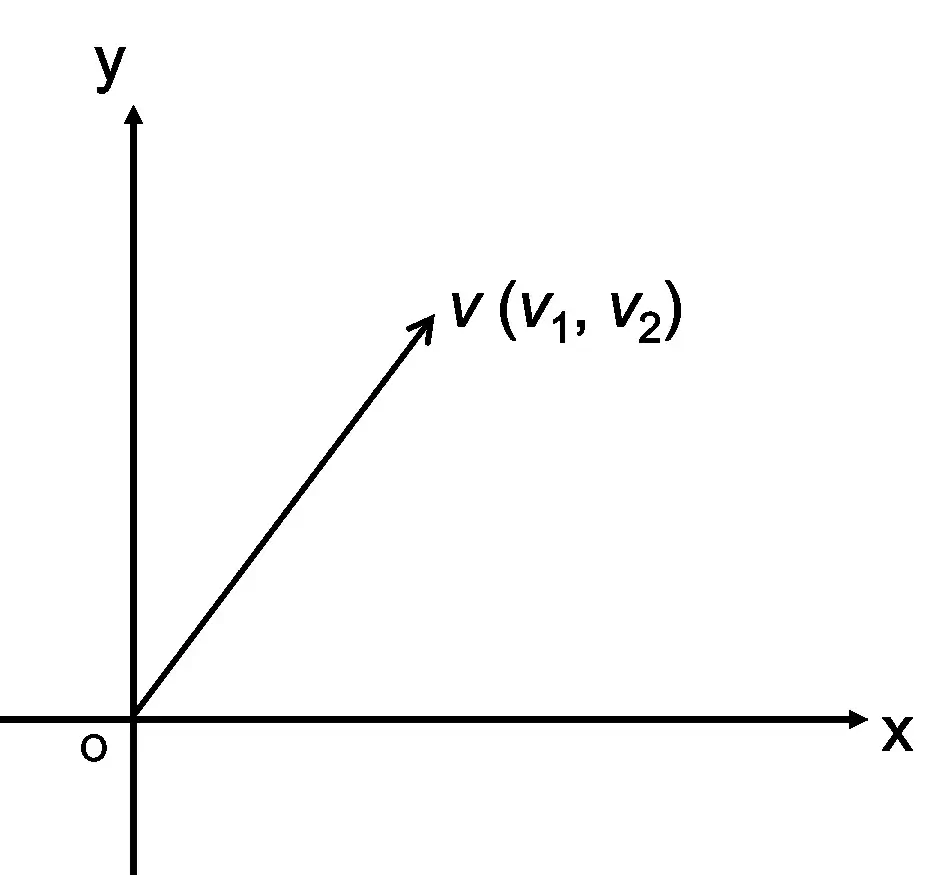
그림은 2차원 $xy$ 좌표계이고, 벡터는 두 성분(component) $v_{1}$, $v_{2}$를 갖습니다.
벡터 $v$는 원점 O (0, 0)에서 점 ($v_{1}$, $v_{2}$)까지의 화살표로 표현됩니다.
보통 벡터는 $v$ = $\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix}$ 또는 $v$ = ($v_{1}$, $v_{2}$) 등으로 씁니다.
2차원 벡터 연산
벡터의 연산을 다시 보겠습니다.
스칼라 곱셈은 다음과 같이, 벡터의 각 성분에 스칼라를 곱해줍니다:
$cv$ = $\begin{bmatrix} cv_{1} \\ cv_{2} \end{bmatrix}$.
예를 들면, 2$v$ = $\begin{bmatrix} 2v_{1} \\ 2v_{2} \end{bmatrix}$ 이고, 이는 $v$ + $v$ 과 같습니다.
스칼라는 다음과 같이 음수도 될 수 있습니다:
$-v$ = $\begin{bmatrix} -v_{1} \\ -v_{2} \end{bmatrix}$. 이 벡터를 다른 벡터에 더하면 사실상 벡터 뺄셈을 해주는 것입니다.
두 벡터 $v$ = $\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix}$ 와 $w$ = $\begin{bmatrix} w_{1} \\ w_{2} \end{bmatrix}$ 이 있다고 가정하면, 두 벡터의 합은
$v$ + $w$ = $\begin{bmatrix} v_{1} + w_{1} \\ v_{2} + w_{2} \end{bmatrix}$ 입니다.
위의 $v$ = $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$, $w$ = $\begin{bmatrix} 2 \\ 3 \end{bmatrix}$ 의 예에서 선형 결합 3$v$ + 5$w$ 는
3$\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ + 5$\begin{bmatrix} 2 \\ 3 \end{bmatrix}$ = $\begin{bmatrix} 3 \\ 3 \end{bmatrix}$ + $\begin{bmatrix} 10 \\ 15 \end{bmatrix}$ =$\begin{bmatrix} 3 + 10 \\ 3 + 15 \end{bmatrix}$ = $\begin{bmatrix} 13 \\ 18 \end{bmatrix}$과 같이 계산할 수 있습니다.
벡터의 연산을 python 프로그램을 이용해서 계산할 수 있는데요.
관심이 있으시면 아래 링크를 참조하시기 바랍니다.
Python과 선형대수: numpy를 이용한 벡터 연산
3차원 벡터 연산
3차원의 경우는 벡터가 다음과 같이 성분을 하나 더 갖습니다:
$v$ = $\begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix}$, $w$ = $\begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix}$.
이 경우도 마찬가지로 벡터를 xyz 공간 좌표계에서 화살표로 그릴 수 있습니다.
두 벡터의 합은 역시 각 성분끼리 더하면 됩니다:
$v$ + $w$ = $\begin{bmatrix} 1 + 2 \\ 1 + 3 \\ -1 + 4 \end{bmatrix}$ = $\begin{bmatrix} 3 \\ 4 \\ 3 \end{bmatrix}$.
선형 결합 (linear combination)
이제 선형 결합의 의미를 좀 더 살펴보겠습니다.
방향이 다른 두 벡터 $v$, $w$ 의 선형 결합 $cv$ + $dw$는 2차원에서는 $xy$ 평면 전체를 채울 수 있습니다. 여기서 채운다는 것은 선형 결합이 $xy$ 평면의 모든 점을 가리킬 수 있다는 것입니다.
3차원에서는 방향이 다른 두 벡터는 평면을 채울 수 있습니다. 이때는 꼭 $xy$ 평면일 필요는 없습니다. 그리고 두 벡터가 만드는 평면에 포함되지 않는 세 번째 벡터를 추가하면, 세 벡터의 선형 결합은 3차원 공간을 채울 수 있습니다.
세 개의 다른 벡터 $u$, $v$, $w$가 있다고 할 때:
1) 한 벡터의 선형 결합 $cu$는 원점을 통과하는 선을 채운다.
2) 두 벡터의 선형 결합 $cu$ + $dv$는 원점을 포함하는 평면을 채운다.
3) 세 벡터의 선형 결합 $cu$ + $dv$ + $ew$는 3차원 공간을 채운다.
이때 세 벡터 모두 다른 벡터들의 선형 결합이 아닙니다.
예를 들어, 두 벡터 $v$ = $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ 와 $w$ =$\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}$ 가 있다고 하면, 선형 결합 $av$ + $bw$는 $xy$ 평면을 채웁니다.
그러면, 다른 두 벡터의 예를 보자. $v$ = $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ 와 $w$’ =$\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}$ 가 있다고 가정하면, 두 벡터의 선형 결합도 역시 $xy$ 평면을 채웁니다.
사실, $w$’는 $v$ 와 w의 합이고, 따라서 선형 결합 $av$ + $bw$’는 $av$ + $b$($v$ + $w$)와 같다.이는 다시 $(a+b)v$ + $bw$ = $a$’$v$ + $bw$ 이므로 $v$ 와 $w$의 선형 결합입니다.
예제 1
세 개의 방정식 $\begin{matrix} c + 2d = 1 \\ c + 3d = 0 \\ c + 4d = 0\end{matrix}$ 은 우변 $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ 이 좌변 $c$$\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ + $d$$\begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix}$의 평면 위에 있지 않기 때문에 해가 없다.
위 방정식들은 다음과 같이 쓸 수 있습니다.
$c$$\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ + $d$$\begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix}$ = $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$
이 방정식이 해를 가지려면, 좌변과 우변이 같아지는 c, d가 존재해야 합니다.
사실 좌변은 두 벡터 $\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$ 와 $\begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix}$의 선형 결합이고, 두 벡터가 만드는 평면으로 표현될 수 있습니다.
따라서 위 방정식이 해를 가지려면 $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$이 그 평면 위에 있어야 합니다.
예제 2
Find two equations for $c$ and $d$ so that the linear combination $cv$ + $dw$ equals $b$:
$v$= $\begin{bmatrix} 2 \\ -1 \end{bmatrix}$, $w$ = $\begin{bmatrix} -1 \\ 2 \end{bmatrix}$, $b$ = $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$.
방정식 $cv$ + $dw$ = $b$ 를 다시 쓰면,
$c$$\begin{bmatrix} 2 \\ -1 \end{bmatrix}$ + $d$$\begin{bmatrix} -1 \\ 2 \end{bmatrix}$ = $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$. => $\begin{bmatrix} 2c \\ -c \end{bmatrix}$ + $\begin{bmatrix} -d \\ 2d \end{bmatrix}$ = $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$. => $\begin{bmatrix} 2c - d \\ -c + 2d \end{bmatrix}$ = $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$.
따라서 찾고자 하는 두 방정식은
–$c$ + $2d$ = 0 과 $2c$ – $d$ = 1 입니다.
이를 계속 풀어보면,
–$c$ + $2d$ = 0에서 $c$ = $2d$. 이를 $2c$ – $d$ = 1 에 대입 하여 풀면, $d$ = 1/3. 다시 $c$ = $2d$ 에서 $c$ = 2/3 임을 알 수 있습니다.
연습 문제 풀이는 아래 링크를 참조하세요.
'선형대수' 카테고리의 다른 글
| 2.1 벡터와 선형 방정식 (Vectors & Linear Equations) (0) | 2022.01.12 |
|---|---|
| 1.3 행렬 (2) (0) | 2022.01.09 |
| 1.3 행렬 (1) (0) | 2022.01.08 |
| 1.2 길이와 내적(dot product) (0) | 2022.01.08 |
| 선형 대수를 공부하고자 하는 분들께 (0) | 2022.01.06 |

댓글