벡터의 내적은 두 벡터의 성분들의 곱의 합으로 정의됩니다. 내적은 두 벡터가 수직하는지, 평행하는지, 또는 둘 사이의 각이 얼마인지 등의 정보를 가지고 있습니다. 또한, 벡터의 길이도 계산할 수 있습니다. 이번 포스팅은 내적을 계산하는 방법, 벡터의 길이, 단위 벡터 등을 다루겠습니다.
내적 (dot product)
두 벡터 $v$ = ($v_{1}$, $v_{2}$)와 $w$ = ($w_{1}$, $w_{2}$)의 내적은 $v$·$w$로 쓰고, $v$·$w$ = $v_{1}w_{1}$ + $v_{2}w_{2}$입니다.
예를 들어, 두 벡터 $v$ = (4, 2)와 $w$ = (–1, 2)가 있다면, 내적은 $v$·$w$ = 4×(–1) + 2×2 = –4 + 4 = 0입니다.
내적이 0이면 두 벡터가 수직임을 의미합니다. 즉, 두 벡터의 각도는 90도입니다.
가장 심플한 예로, 2차원 단위 벡터 $i$ = (1, 0)와 $j$ = (0, 1)도 수직입니다. $i$는 $x$축의 단위 벡터이고 $j$는 $y$축의 단위 벡터입니다. 이 경우도 두 벡터의 내적은 0이다. 나중에 단위 벡터에 대해 자세히 알아볼 것입니다.
만약 내적에서 $v$와 $w$의 순서를 바꾸면 어떻게 될까요?
$w$·$v$를 계산해 보겠다. $w$·$v$ = $w_{1}v_{1}$ + $w_{2}v_{2}$이고, 사실 이것은 $v_{1}w_{1}$ + $v_{2}w_{2}$와 같습니다.
이는 $v$·$w$ = $w$·$v$를 의미합니다.
일반적으로 n차원에서 두 벡터 $v$와 $w$의 내적은 $v$·$w$ = $v_{1}w_{1}$ + $v_{2}w_{2}$ + … + $v_{n}w_{n}$입니다.
n번째 성분까지 계산 합니다.
다음은 벡터가 자기 자신과 내적을 할 경우입니다.
2차원: $v$·$v$ = $v_{1}v_{1}$ + $v_{2}v_{2}$ = $v_{1}^{2}$ + $v_{2}^{2}$.
n차원: $v$·$v$ = $v_{1}v_{1}$ + $v_{2}v_{2}$ +… + $v_{n}v_{n}$ = $v_{1}^{2}$ + $v_{2}^{2}$ + … + $v_{n}^{2}$.
벡터의 길이
벡터 v = (1, 2, 3)가 있다고 가정합시다.
그러면,$v{\cdot}v$ = (1, 2, 3)∙(1, 2, 3) = 12 + 22 + 32 = 14
사실, 이 값은 벡터 $v$의 길이 (||$v$||)의 제곱입니다.
아래의 그림은 2차원의 예입니다.
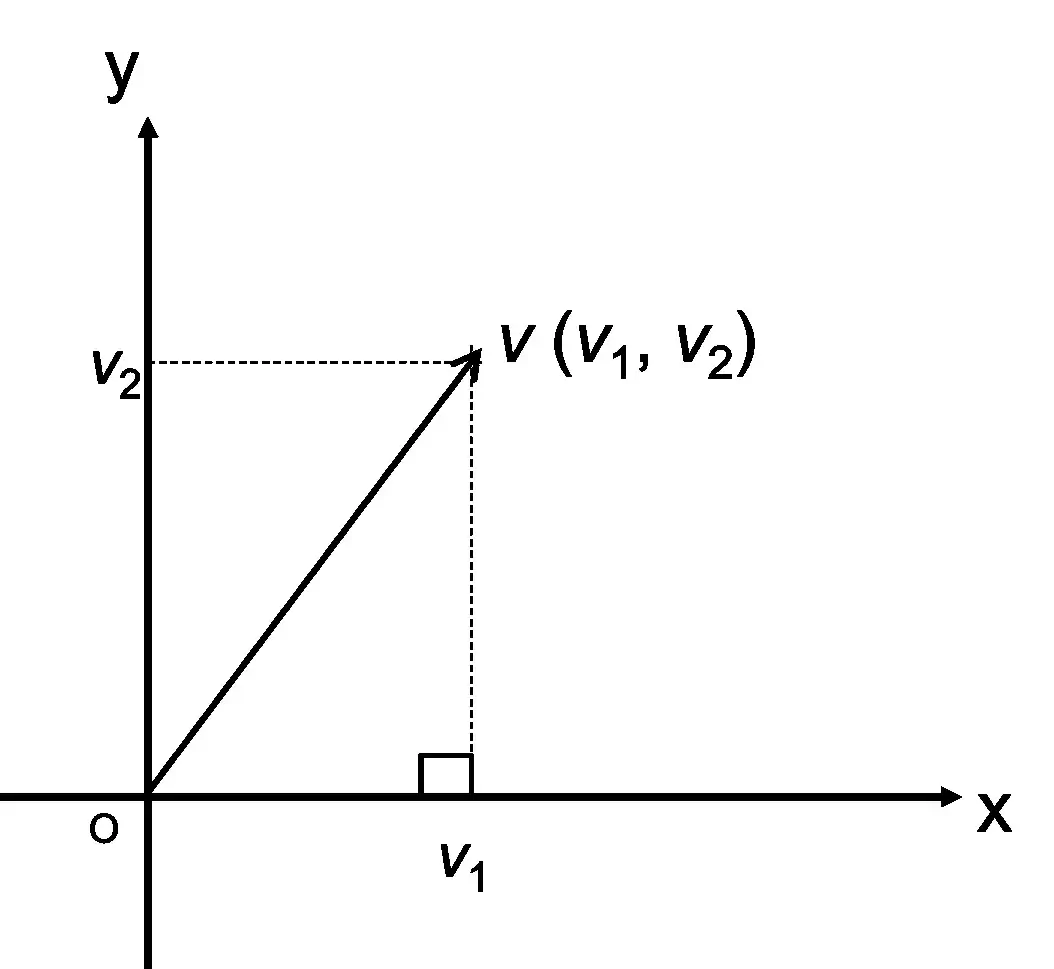
그림에서 화살표의 길이는 벡터의 길이입니다.
피타고라스의 공식 (||$v$||2 = $v_{1}^{2}$ + $v_{2}^{2}$)에 의해 $v$의 길이는 다음과 같이 $v{\cdot}v$의 제곱근이 됩니다.
||$v$||2 = $v_{1}^{2}$ + $v_{2}^{2}$ = $v{\cdot}v$ → ||$v$|| = $\sqrt{v{\cdot}v}$
이런 식으로, 3차원의 경우 벡터 $v$ = ($v_{1}$, $v_{2}$, $v_{3}$)의 길이는 $v_{1}^{2}$ + $v_{2}^{2}$ + $v_{3}^{2}$ (또는 $v{\cdot}v$)의 제곱근입니다.
n차원의 경우, 벡터의 길이는 다음과 같이 정의됩니다.
DEFINITION 벡터 $v$의 길이 ||$v$||는 $v{\cdot}v$의 제곱근이다.
||$v$|| = $\sqrt{v{\cdot}v}$ = ($v_{1}^{2}$+ $v_{2}^{2}$+⋯+ $v_{n}^{2}$)$^{1/2}$.
예) 두 벡터 $v$ = (1, 3, 2)와 $w$ = (4, –4, 4)가 있다 가정하자.
두 벡터의 내적은 $v$·$w$ = 1·4 + 3·(–4) + 2·4 = 4 –12 + 8 = 0.
내적이 0이기 때문에 두 벡터는 수직 합니다.
또한 벡터 $v$의 길이는 $v{\cdot}v$의 제곱근으로 다음과 같이 구할 수 있습니다:
$v{\cdot}v$ = (1, 3, 2)·(1, 3, 2) = 1·1 + 3·3 + 2·2 = 1 + 9 + 4 = 14.
→ ||$v$|| = $\sqrt{14}$.
단위 벡터 (unit vector)
DEFINITION 단위 벡터 $u$는 길이가 1인 벡터입니다. 즉, $u{\cdot}u$ = 1.
다음 4차원 벡터의 예를 보자:
$u$ = (1/2, 1/2, 1/2, 1/2).
$u$∙$u$를 계산하면,
$u$∙$u$ = 1/2∙1/2 + 1/2∙1/2 + 1/2∙1/2 + 1/2∙1/2 = 1/4 + 1/4 + 1/4 + 1/4 = 1.
이 내적의 제곱근 역시 1이기 때문에, $u$는 길이가 1입니다.
따라서, $u$는 단위 벡터입니다.
반면에, $v$ = (1, 1, 1, 1)는 단위 벡터가 아닙니다.
길이가 2인 벡터이기 때문입니다. (||$v$||2 = $v{\cdot}v$ = 12 + 12 + 12 + 12 = 4)
하지만, v를 자신의 길이 ||$v$||로 나눠준 $v$/||$v$||는 길이가 1인 벡터가 되고, 따라서 단위 벡터입니다.
2차원 단위 벡터
표준 단위 벡터 $i$ = (1, 0), $j$ = (0, 1)
$u$ = (cosθ, sinθ)
$u$의 길이는 $u{\cdot}u$ = cos2θ + sin2θ = 1에서, 1 임을 알 수 있습니다.
여기서 θ는 벡터와 $x$축의 각입니다.
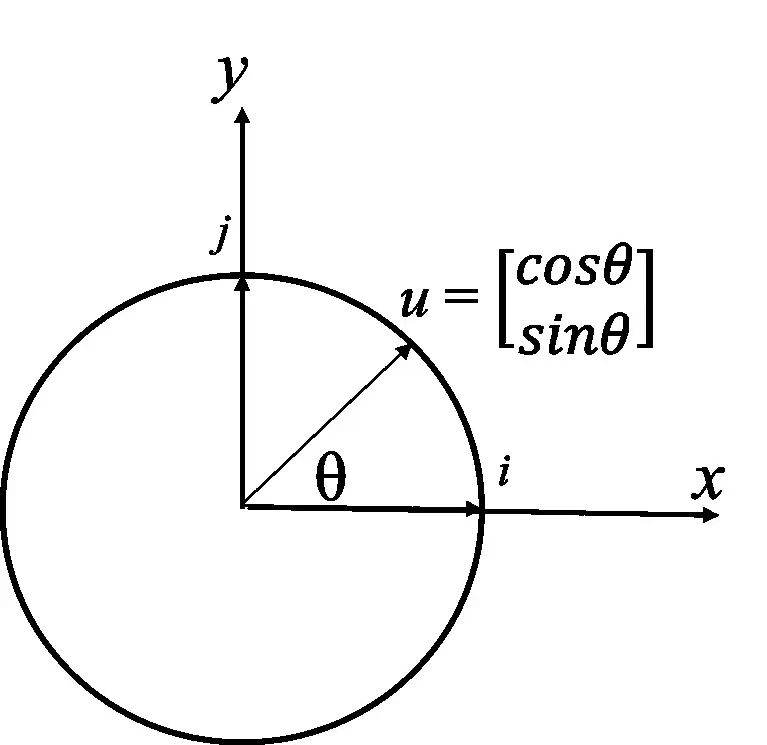
위 단위원 상의 모든 벡터는 길이가 1이므로 단위 벡터가 됩니다.
코사인 식 (cosine formula)
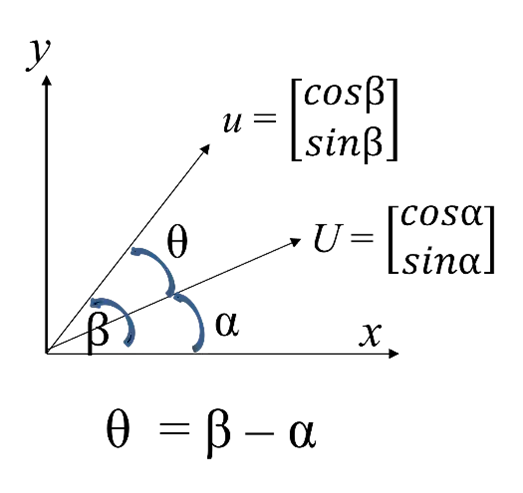
위 그림에서 벡터 $u$와 $U$는 단위 벡터입니다.
두 벡터 사이의 각은 θ이고, θ = β – α입니다.
이때, 두 벡터의 내적은 $u{\cdot}U$ = cos θ 이 됩니다.
유도 과정) $u$ = (cosβ, sinβ), $U$ = (cosα, sinα), β = α + θ.
$u{\cdot}U$ = cosβcosα + sinβsinα = cos(α + θ)cosα + sin(α + θ)sinα.
여기서 다음 삼각함수 공식을 사용합니다:
sin(x+y) = sinxcosy + cosxsiny.
cos(x+y) = cosxcosy – sinxsiny.
그러면, $u{\cdot}U$ = cos2αcosθ – sinαsinθcosα + sin2αcosθ + cosαsinθsinα
= (cos2α + sin2α)cosθ = cosθ
따라서, 사이각이 θ인 두 벡터 $v$와 $w$는 다음을 만족합니다:
$\frac{v{\cdot}w}{||v||||w||}$ = cosθ
슈와르츠 부등식 (Schwarz inequality) & 삼각 부등식 (Triangle inequality)
코사인 함수는 1에서 –1 사이의 값을 가집니다.
즉, |cosθ| ≤ 1 이기 때문에, 위에서 본 코사인 식을 이용하면 다음의 슈와르츠 부등식을 얻습니다:
|$\frac{v{\cdot}w}{||v||||w||}$| ${\leq}$ 1 → $\frac{|v{\cdot}w|}{||v||||w||}$ ${\leq}$ 1
→ $|v{\cdot}w|$ ${\leq}$ $||v||||w||$ – 슈와르츠 부등식
삼각형에서 한 변의 길이가 다른 두 변의 합보다 클 수 없다는 삼각 부등식은 벡터의 길이를 이용하여 다음과 같이 쓸 수 있습니다.
||$v$ + $w$|| ≤ ||$v$|| + ||$w$||
1장2절의 연습문제는 아래 링크를 참조하세요.
1.2a 벡터의 내적 관련 연습 문제(1~5)
1.2절 벡터의 내적과 관련된 연습 문제를 풀어보겠습니다. 1. 다음 벡터들의 내적 $u$ · $v$, $u$ · $w$, $u$ · ($v$ + $w$), $w$ · $v$를 계산하라. $u$ = $\begin{pmatrix} \begin{array}{r} -.6 \\ .8 \end{array} \end{pmatrix}$,
er5030000.tistory.com
1.2b 벡터들이 이루는 각과 내적에 관한 연습 문제(6~9)
1.2b 벡터들이 이루는 각과 내적에 관한 연습 문제(6~9)
벡터들이 이루는 각과 내적에 관한 연습 문제를 풀겠습니다. 특히 두 벡터가 수직인 경우(내적이 0)인 경우의 문제가 많습니다. 6. (a) 벡터 $v$ = (2, –1)에 수직인 모든 벡터 $w$ = ($w_{1}$, $w_{2}$)를
er5030000.tistory.com
1.2c 벡터의 내적과 각, 수직에 대한 연습 문제(10~14)
1.2c 벡터의 내적과 각, 수직에 대한 연습 문제(10~14)
벡터의 내적과 벡터의 각(수직)에 관련된 연습 문제들을 풀어보겠습니다. 연습 문제와 관련하여 다음 링크를 참조하시기 바랍니다. 1.2 길이와 내적(dot product) 10. (0, 0)에서 점 $v$ = (1, 2) 및 $w$ = (-2
er5030000.tistory.com
1.2d Schwarz 부등식, 벡터의 각, cosθ 등에 관한 연습 문제(15~17)
1.2d Schwarz 부등식, 벡터의 각, cosθ 등에 관한 연습 문제(15~17)
15. Schwarz 부등식, 산술평균, 기하평균 문제. $x$ = 2와 $y$ = 8의 기하평균은 $\sqrt{xy}$ = 4입니다. 산술 평균은 $\frac{1}{2}$($x$ + $y$) = __ 으로 기하평균보다 큽니다. 이것은 $v$ = ($\sqrt{2}$, $\sqrt{8}$) 및 $w$ =
er5030000.tistory.com
1.2e 피타고라스 정리, 삼각부등식 등(18~22)
1장 2절 피타고라스 정리, 삼각부등식, 슈와르츠 부등식 등에 관한 문제 풀이입니다. 문제 18. 피타고라스 정리 변 $v$ = (4, 2)와 $w$ = (−1, 2)로 이루어진 평행사변형은 직각 사각형입니다. 직각삼각
er5030000.tistory.com
'선형대수' 카테고리의 다른 글
| 2.1 벡터와 선형 방정식 (Vectors & Linear Equations) (0) | 2022.01.12 |
|---|---|
| 1.3 행렬 (2) (0) | 2022.01.09 |
| 1.3 행렬 (1) (0) | 2022.01.08 |
| 1.1 벡터 (vector) & 선형 결합 (linear combination) (0) | 2022.01.06 |
| 선형 대수를 공부하고자 하는 분들께 (0) | 2022.01.06 |

댓글