이번 포스팅에서는 방정식이 세 개, 미지수도 세 개인 연립 방정식 문제를 소거법으로 풀어 보겠습니다. 소거법으로 방정식들의 미지수를 차례로 제거하여 상부 삼각형 시스템을 만드는 것이 목적입니다. 그러면 피벗과 방정식의 해를 쉽게 구할 수 있습니다.
소거법 - 세 개의 방정식, 세 개의 미지수
이제 방정식이 세 개, 미지수도 세 개인 예를 살펴보겠습니다.
$\begin{matrix} \begin{array}{rrrrrrrr} 2x & + & 4y & - & 2z & = & 2 & (eq. 1) \\ 4x & + & 9y & - & 3z& = & 8 & (eq. 2) \\ -2x & - & 3y & + & 7z & = & 10 & (eq. 3) \end{array} \end{matrix}$
(나중에 설명하겠지만, 이 문제는 3 × 3 행렬과 대응됩니다. 일단, 3 × 3 예라고 합시다)
앞서서 봤던 2 × 2 예와 마찬가지로 소거법으로 2번 방정식에서 $x$항, 3번 방정식에서 $x$와 $y$항들을 차례로 제거하여, 상부 삼각형을 만들 것입니다.
먼저 1번 방정식으로 2번 방정식의 $4x$를 제거합니다.
1번 방정식의 첫 번째 미지수 $x$의 계수 2가 첫 번째 피벗이 됩니다.
제거하려는 $4x$의 4에서 첫 번째 피벗 2를 나눠주어 multiplier는 2가 됩니다.
따라서 2번 방정식 – multiplier × 1번 방정식을 하면 2번 방정식의 $4x$가 제거 되고 $y + z = 4$가 남게 됩니다.
다음은 같은 방식으로 3번 방정식에서 $x$와 $y$항을 제거합니다:
3번 방정식 – (–1) × 1번 방정식 → $y$ + $5z$ = 12가 남습니다.
다시, ($y$ + $5z$ = 12) – 1 × ($y$ + $z$ = 4) → $4z$ = 8가 남습니다.
최종적으로 소거 후 남은 방정식들을 모아보면 다음과 같이 상부 삼각형이 됩니다.
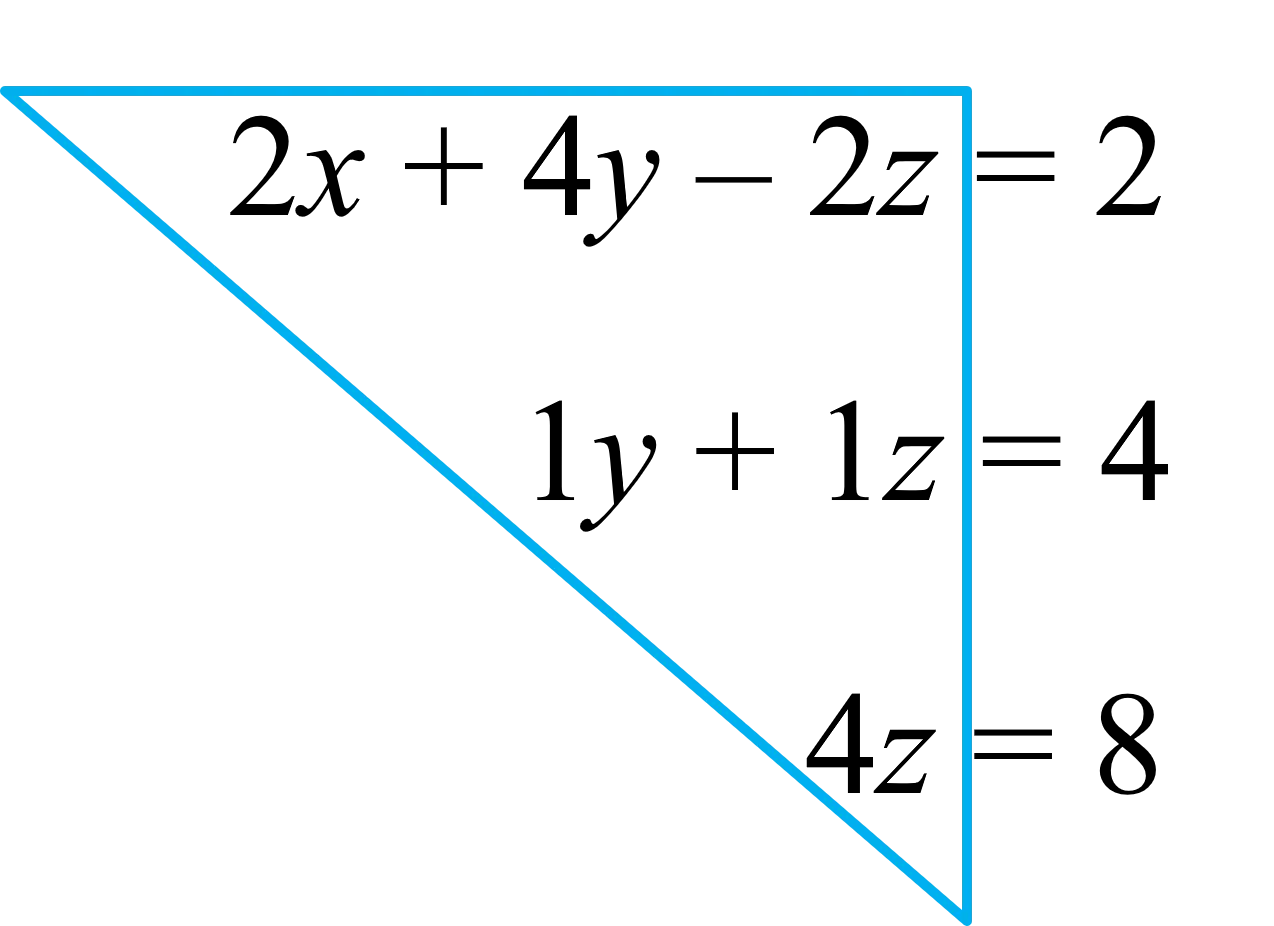
세 번째 방정식에서 $z$ = 2를 쉽게 얻을 수 있고,
이 값을 위에 식들에 차례로 대입하여 $y$ = 2와 $x$ = –1을 계산하여 해를 구할 수 있습니다.
즉, 방정식의 해는 ($x$, $y$, $z$) = (–1, 2, 2)입니다.
또한, 위 그림에서 첫 번째 피벗은 2, 두 번째 피벗은 1, 그리고 세 번째 피벗은 4 임을 알 수 있습니다.
이보다 방정식과 미지수의 수가 많은 4 × 4, 5 × 5, …의 문제들도 같은 방식으로 상부 삼각형이 나올 때까지 소거를 진행하여 풀 수 있습니다.
Row picture & column picture
위 예를 2.1절에서 배운 row picture와 column picture로 보면 다음과 같습니다.
Row picture: 위 세개의 방정식들은 3차원 좌표계에서 각각 평면 방정식과 대응됩니다.
그리고, 점 ($x$, $y$, $z$) = (–1, 2, 2)는 세 평면의 교점입니다.
소거법으로 2번과 3번 방정식의 평면은 달라지지만 교점은 변함이 없습니다.
Column picture: 위 예에서 좌변은 다음과 같이 세 벡터의 선형 결합입니다:
(–1)$\begin{bmatrix} \begin{array}{r} 2 \\ 4 \\ -2 \end{array} \end{bmatrix}$ + 2$\begin{bmatrix} \begin{array}{r} 4 \\ 9 \\ -3 \end{array} \end{bmatrix}$ + 2$\begin{bmatrix} \begin{array}{r} -2 \\ -3 \\ 7 \end{array} \end{bmatrix}$
여기서, 벡터들의 계수는 해 (–1, 2, 2)입니다.
그리고 이 선형 결합은 우변에 대응하는 벡터 $\begin{bmatrix} \begin{array}{r} 2 \\ 8 \\ 10 \end{array} \end{bmatrix}$과 같습니다.
소거 후에는 (–1)$\begin{bmatrix} \begin{array}{r} 2 \\ 0 \\ 0 \end{array} \end{bmatrix}$ + 2$\begin{bmatrix} \begin{array}{r} 4 \\ 1 \\ 0 \end{array} \end{bmatrix}$ + 2$\begin{bmatrix} \begin{array}{r} -2 \\ 1 \\ 4 \end{array} \end{bmatrix}$ = $\begin{bmatrix} \begin{array}{r} 2 \\ 4 \\ 8 \end{array} \end{bmatrix}$로 선형 결합에서 계수들은 변함없습니다.
'선형대수' 카테고리의 다른 글
| 2.3 치환행렬(Permutation matrix) & 첨가행렬(Augmented matrix) (0) | 2022.01.17 |
|---|---|
| 2.3 행렬에 소거법 적용하기 (0) | 2022.01.16 |
| 2.2 소거법 (Elimination) (1) (0) | 2022.01.13 |
| 2.1 벡터와 선형 방정식 (Vectors & Linear Equations) (0) | 2022.01.12 |
| 1.3 행렬 (2) (0) | 2022.01.09 |


댓글